Area Is Essential for Euclidean Geometry
summary
Our eyes can receive only discrete photons. As a logical consequence, the first image at our eyes resembles the 2D raster image closely. However, our visual system intelligently creates the 3D vector image from the 2D raster image. Therefore, our brain creates the Euclidean space.
Does a Point Exist?
What is a point? This problem was considered profoundly in ancient Greece. Euclid defined a point in
Elements as follows. A line is breadthless length: the definition 2 of BookⅠ. The ends of a line are points: the definition 3 of BookⅠ. These definitions mean that a point has no area and no length. Euclid might presumably notice that a point does not actually exist on a line in the Euclidean space. We cannot detect a point on a line or an isolated point because a point has no detectable extent. However, if a point is the end of a line, we can recognize a point. Therefore, a potentially existing point is actualized as the end of a line. Additionally, a point can be ends of multiple lines. Figure 1 shows the actualization of points by cuts of lines:
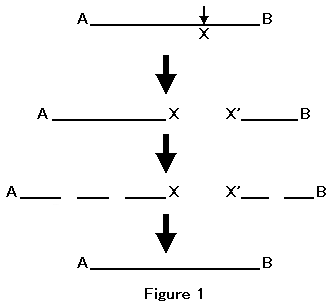
Point X potentially exists on the line AB. If the line AB is cut into two line segments, then potential point X is cut into actual points: X and X'. No matter how many times line AB is cut, the sum of lengths of resulting line segments stay constant. It equals the length of the line AB. Then, we can restore line AB. At the time, actual two points are merged into one potential point. Figure 2 shows that no matter how many points are merged, the sum of lengths of points equals zero:
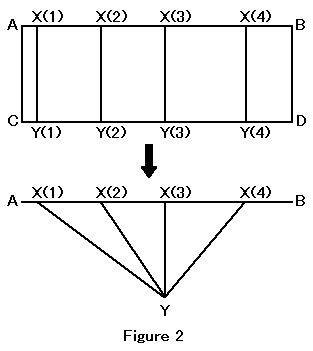
There are two straight lines: AB and CD. They have the same length and ABDC is a rectangle. There is a one-to-one correspondence between points on AB and points on CD. The upper part of Figure 2 shows that the perpendicular line links a point on AB to the correspondent point on CD. The lower part of figure 2 shows that we can merge points on CD into one point despite the number of actualized points. This means that actualization of points does not reduce the sum of lengths of resulting lines and then potentially infinite points are left on resulting lines. That is, we cannot complete the actualization of points on AB. In other words, actualization of points does not reduce potentially existing points on lines. This means that a line does not con sist of points.
Our Eyes Can Recognize Only a Surface
What is a line? This is the next important question. Euclid defined a line in Elements as follows. A surface is that which has length and breadth only: definition 5 in
BookⅠ. The edges of a surface are lines: definition 6 in BookⅠ. These definitions seem unnatural. A line is defined on the basis of a surface. Moreover, a point is defined on the basis of a line. That is to say, Euclid defined the simpler concept by the relation to the more complex concept. This means that a surface is essential for Euclidean geometry. Our eyes can recognize only a surface because only a surface can reflect light. By contrast, a point and a line cannot reflect light. Additionally, we cannot recognize directly a solid. Instead, our visual system needs to construct a 3-dimensional object from surfaces. The extraction of the edge is the important step for the task and the edge of the surface is the Euclidean line. Then, we shall discuss features of a line in relation to a surface. Figure 3 shows that a square is cut into four rectangles.
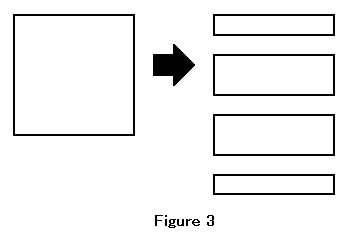
In this case, six lines are actualized, but the sum of areas does not change. This means that an area does not consist of lines. That is, lines have no area. So, we cannot recognize directly a line. However, we can recognize a line as the edge of a surface or as the boundary of areas. Equally, we can recognize a point as the end of a line. Then, the relationship between a surface and a line is identical to the relationship between a line and a point.
A Line Is a Boundary of Two Areas
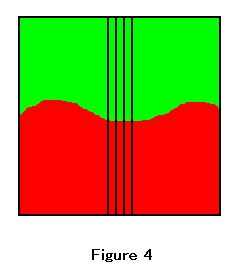
In plane geometry, an Euclidean line is a pure boundary of two areas. Figure 4 shows the green area and the red area. The boundary of these areas is a line.
Generally, an area is measured in square units. We can consider that an area consists of very small squares. This idea can be applied also to the area enclosed by the curve. This is the partition of unity quadrature. In figure 4, the whole area can be equally divided into very thin rectangles. The figure shows only three of the rectangles. We shall zoom the boundary part of a rectangle. Figure 5 shows the expanded image of the boundary part.
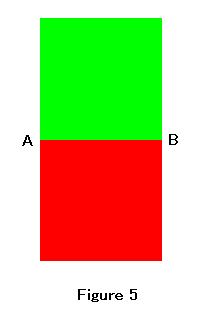
In this scale, we can approximate the curve by the straight line. Figure 5 shows the green square and the red square. In the figure, the line AB has no area and no substance. Hence we can recognize a line only as the boundary of two areas.
Where Did the Unit Square Go Away to?
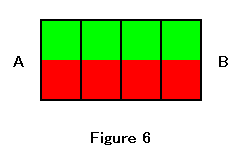
The minimum area is necessary so that the surface can reflect light. First, if we assume that the unit square has the indivisible minimum area, then we can consider that area consists of unit squares. Second, we define a line as the boundary of the area. Third, we can define the basic unit of length as a side of the unit square. Figure 6 shows that the line AB is the boundary between the green area and the red area.
In figure 6, the length of the line AB is four units of length. This sequence of definition seems natural. If we assume the indivisible minimum area, we can use this logic. For practical use, we can determine the unit square corresponding to required accuracy. Theoretically, we can use an arbitrary square as the unit square. However, we cannot detect the unit square in the
Euclidean space. So, we regard the Euclidean space as continuous. Consequently, the Euclidean space cannot consist of indivisible unit squares. Where did the unit square go away to?
Our Brain Creates the Euclidean Space
Donald D. Hoffman says in
Visual Intelligence "Vision is not merely a matter of passive perception, it is an intelligent process of active construction. What you see is, invariably, what your visual intelligence constructs". Hoffman describes that the first image at your eyes is discrete. So, the first image resembles the 2D
raster image closely. The raster image consists of
pixels. The pixel can correspond to the unit square. However, our visual system intelligently constructs our visual world based on the first image. That is, our visual intelligence creates the 3D
vector image from the 2D raster image. In this process, the visual intelligence conceals the unit square from our consciousness. Even so, the visual intelligence implicitly uses the unit square as length. In conclusion, our brain creates the Euclidean space. There is a more detailed discussion in
The Biological Foundation of Geometry.
Table of Contents